Математические модели в оценке рисков портфеля

Movchan тобы

Jun 27, 2023

В основе многих стратегий на финансовом рынке лежит математика. Данные о ценах активов и корреляции между ними позволяют анализировать историческую доходность и уровень риска, а также оценить вероятность прибыли или убытков в будущем. Рассказываем подробнее, как инвестор может использовать математику.

Зачем оценивать риски портфеля

Прибыль на бирже не может быть гарантирована: инвестор может лишь предполагать ожидаемую доходность на основе исторических данных о ценах активов и прогнозов будущих событий. Оценка рисков помогает определить возможное отклонение результатов от ожидаемых — как в сторону большей прибыли, так и в сторону снижения доходности или убытков. Если диапазон этого отклонения велик, портфель можно назвать рискованным. Поэтому оценка рисков также помогает инвестору определить, соответствует ли собранный портфель его риск-профилю и готов ли он рисковать в такой степени.

Риски портфеля складываются из рисков входящих в него активов, но не линейно. Активы в портфеле имеют свои уникальные риски и их влияние на риски портфеля зависят от взаимодействия между собой. Например, цены акций и золота могут значительно колебаться, но в разные фазы экономического цикла эти риски могут компенсировать друг друга. Так, во время кризиса на фондовом рынке цены акций падают, а цена золота, как правило, растет. Именно поэтому в портфеле важна диверсификация — разделение капитала между активами с разным рисками, не связанными между собой.

Существуют разные типы рисков активов:

• Рыночный риск. Вероятность снижения цены актива из-за колебаний на рынке в целом. Из-за макроэкономических, геополитических и других факторов инвесторы доверяют фондовому рынку то больше, то меньше: это влияет на цены большинства активов.
• Отраслевой риск. Цена акции зависит от ситуации в отрасли, в которой работает компания. Если отрасль сталкивается с проблемами, например, снижением спроса или подорожанием сырья, оценка компаний инвесторами может снизиться.
• Кредитный риск. В случае с государственными и корпоративными облигациями есть риск, что эмитент не сможет выполнить долговые обязательства.
• Процентный риск. При росте ожиданий по ставкам доходности облигаций тоже будут расти.
• Валютный риск. Если капитал распределен между активами, номинированными в разных валютах, есть риск изменения их обменных курсов. Даже если у актива растет номинальная доходность, реальная доходность может быть меньшей из-за курсовой разницы.
• Риск ликвидности. Активы не всегда можно продать по цене близкой к рыночной. Это называют низкой ликвидностью и владелец таких активов несет риски потерь при необходимости быстрой продажи.
• Страновой (геополитический) риск. Войны, революции, политические кризисы, санкции и другие масштабные события повышают экономическую неопределенность. Активы стран с высокими геополитическими рисками могут принести инвестору убытки.
• Инфляционный риск. Реальная доходность инвестиций рассчитывается за вычетом инфляции. Если инфляция растет, реальная доходность некоторых активов может стать меньшей или вовсе отрицательной несмотря на номинальную прибыль.

Для правильной оценки рисков портфеля необходимо определить и оценить различные риски активов, выявить корреляцию между ними и спрогнозировать доходность в различных рыночных ситуациях. Для этого и используют математические модели — методы количественной оценки рисков портфеля.

Показатели оценки риска

Математические модели для оценки рисков портфеля

Математические модели позволяют рассчитать, насколько сильно будет колебаться доходность, как разные активы в портфеле связаны между собой и сколько инвестор может потерять при негативном сценарии. Это помогает принимать более обоснованные инвестиционные решения и создать портфель с приемлемым уровнем риска. Рассмотрим несколько популярных у инвесторов математических моделей.

Модель оптимального портфеля Марковица

Модель Марковица (Mean-Variance Model) помогает найти наилучшее сочетание активов в портфеле, при котором риск портфеля будет минимальным, а ожидаемая доходность — не ниже заданной. Эту модель создал Гарри Марковиц — американский экономист, лауреат Нобелевской премии по экономики и основатель современной теории портфелей.

С точки зрения математики эта модель решает задачу оптимизации. Она перебирает все возможные комбинации активов, чтобы найти вариант с минимальным риском при заданной ожидаемой доходности или вариант с максимальной доходностью при заданном уровне риска. Поскольку риск рассчитывается с помощью квадратичной функции, этот способ также называют задачей квадратичного программирования.

Риск портфеля в модели Марковица считается по формуле:

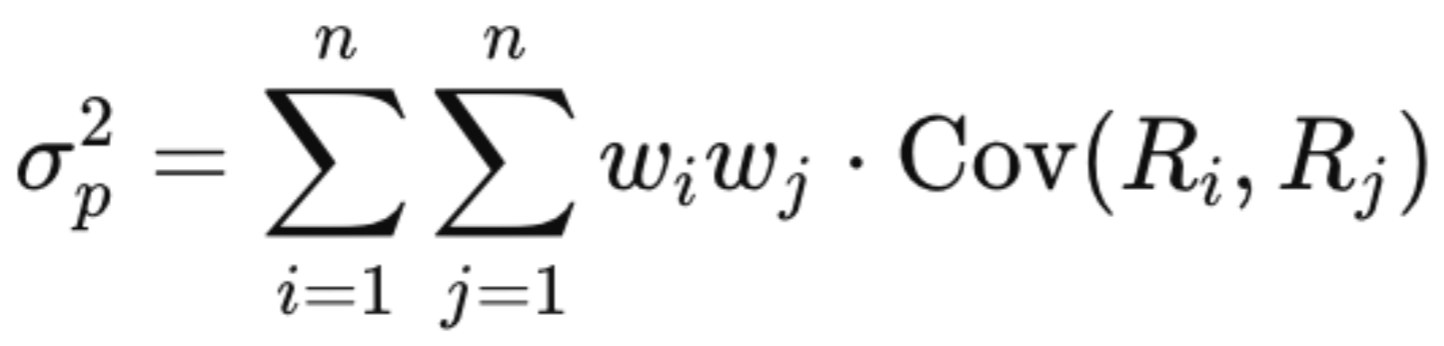
• σp2— дисперсия доходности портфеля (стандартное отклонение в квадрате — мера риска портфеля)

• n — количество активов в портфеле (все активы в портфеле получают нумерацию i и j, чтобы модель сравнивала их попарно)

• wi​ — доля i-го актива в портфеле от 0 до 1 (например, если актив занимает 60%, wi​ = 0,6)
• wj​ — доля j-го актива в портфеле от 0 до 1
• Cov (Ri ,Rj ) — ковариация доходностей между каждой парой активов

Эта формула учитывает риски каждого актива в отдельности, а также ковариацию каждой пары активов — показатель того, насколько их доходности изменяются похожим образом. Если доходности растут или падают вместе, ковариация положительная, если доходности изменяются в разные стороны, ковариация отрицательная. Отрицательная ковариация активов снижает общий риск портфеля: именно на этом основана диверсификация.

Помимо рисков разных комбинаций долей активов модель Марковица также рассчитывает ожидаемые доходности каждого варианта портфеля по формуле:

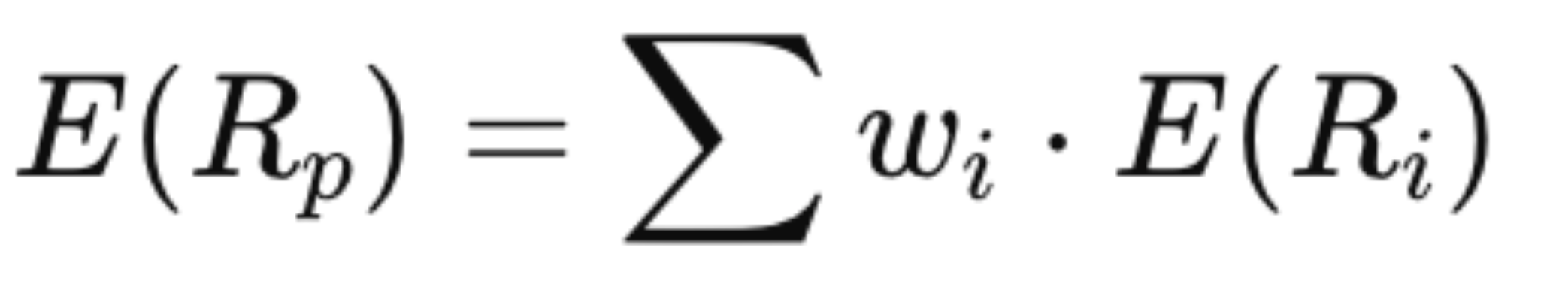
• E(Rp) — ожидаемая доходность портфеля в процентах за рассматриваемый период (например, год)
•  wi​ — доля i-го актива в портфеле от 0 до 1
• E(Ri) — ожидаемая доходность i-го актива за рассматриваемый период

После этого модель отбрасывает комбинации активов, которые не соответствуют заданной доходности или уровню риска. В результате инвестор получает модель портфеля, в которой риски будут минимальными (или будет максимальной доходность). Найденный вариант называют “оптимальным портфелем по Марковицу” — в нем будет наилучшее соотношения риска и доходности при заданных ограничениях.

Вместо четко заданных ограничений (например, “максимальный уровень риска — 10%”), можно сравнить множество возможных вариантов портфелей с разными ограничениями. Для этого строится график зависимости риска и доходностей с разными вариантами портфеля на кривой.

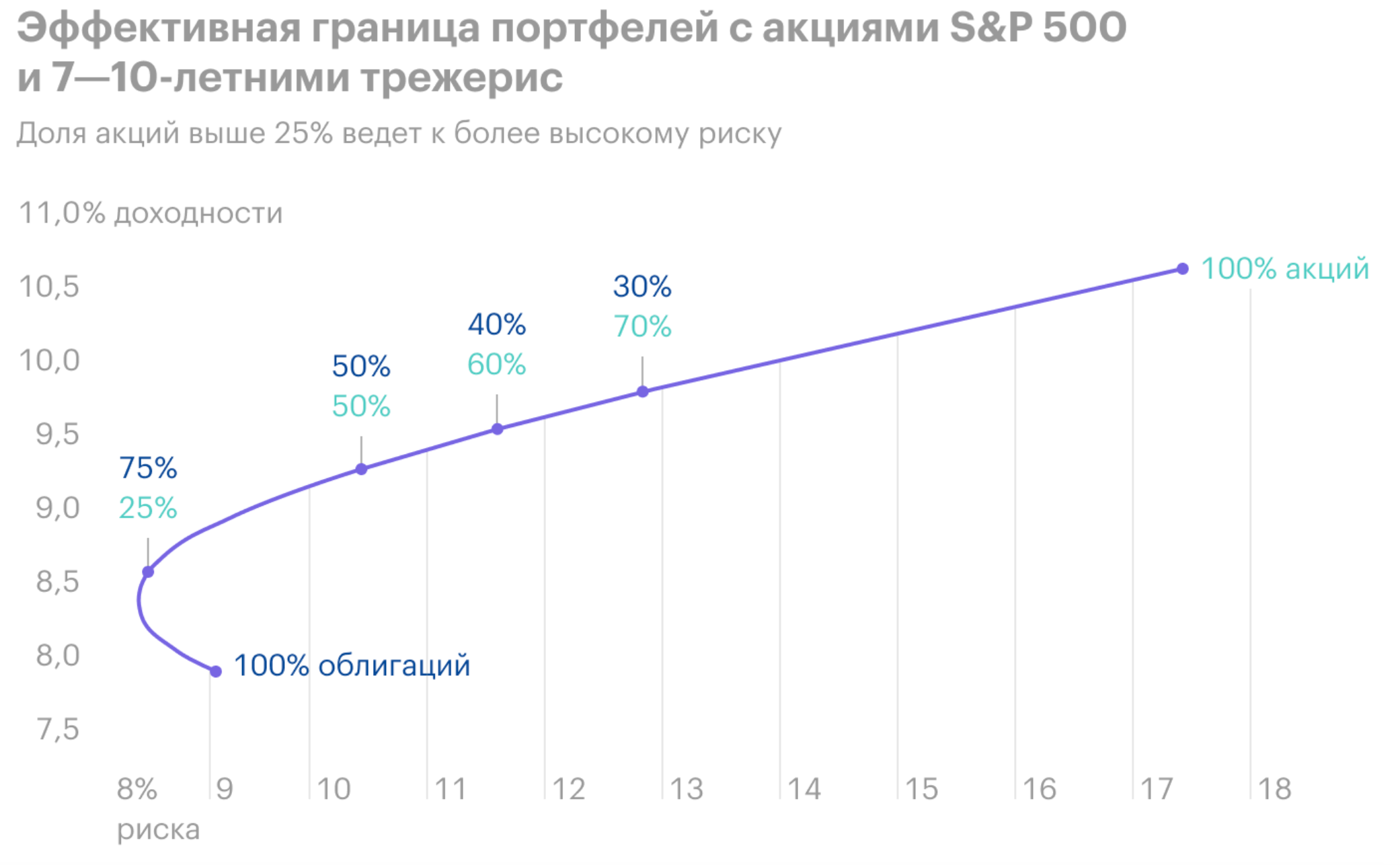
Источник: Т—Ж

Верхняя выпуклая часть кривой — это эффективная граница портфелей, на которой расположены все оптимальные варианты. Выше этой границы не существует портфелей с таким соотношением доходности и риска. При этом ниже границы находятся неоптимальные портфели с меньшей доходностью и большим риском.

На эффективной границе инвестор может выбрать подходящий портфель при разном ожидаемом риске или доходности. Например, комбинация 30% облигаций и 70% акций даст бóльшую доходность, но рисков будет меньше у комбинации 75% облигаций и 25% акций.

Модель капитального ценообразования (CAPM)

Модель CAPM (Capital Asset Pricing Model) показывает, какую доходность должны приносить активы в портфеле, чтобы компенсировать инвестору связанные с ними риски. В отличие от модели Марковица, с помощью CAPM нельзя подобрать оптимальный портфель по уровню риска, но можно оценить риски уже собранного портфеля. Модель капитального ценообразования создана другим Нобелевским лауреатом, американским экономистом Уильямом Шарпом.

Эта математическая модель оценивает, насколько ожидаемая доходность портфеля пропорциональна уровню риска, который нельзя устранить с помощью диверсификации. Такой риск называют систематическим, то есть связанным с факторами рынка в целом, и оценивают с помощью бета-коэффициента. 

Основная формула в CAPM выглядит так:

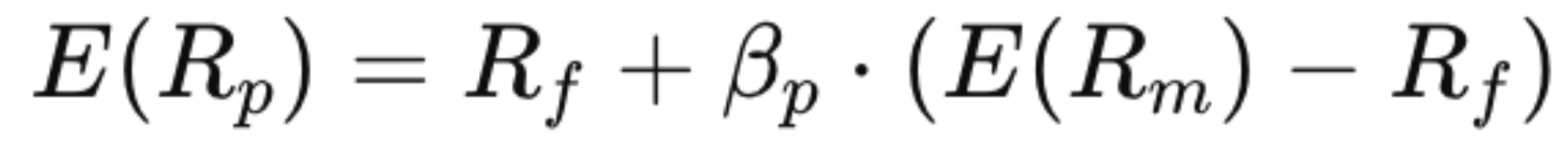
• E(Rp) — ожидаемая доходность портфеля
• Rf — безрисковая ставка (например, доходность по гособлигациям США)
• βp — бета-коэффициент портфеля (мера чувствительности доходности портфеля к изменению цен на рынке)
• E(Rm) — ожидаемая доходность рыночного портфеля (например, созданного из акций из индекса S&P 500

Бета-коэффициент (β) показывает, насколько сильно актив реагирует на изменения цен на всем рынке. Если включать в портфель активы с разной бета, его зависимость от общего направления рынка, а значит и риски — снизятся. 

Бета рассчитывается по сравнению с рыночным ориентиром, чаще всего с индексом S&P 500. Для этого используют исторические данные о ценах актива и индекса за много лет. Уже рассчитанные значения бета для каждого актива можно найти на аналитических финансовых сайтах, например Yahoo Finance и Google Finance. Бета портфеля рассчитывается как взвешенная сумма бета-коэффициентов всех активов, входящих в портфель, то есть с учетом их долей в портфеле.

Одни активы растут и падают вместе с индексом, другие — колеблются слабее или вообще движутся независимо. Поэтому, чем лучше активы в портфеле диверсифицированы по бете, тем меньше риск просадок. Вот какие значения может принимать бета-коэффициент у разных активов:

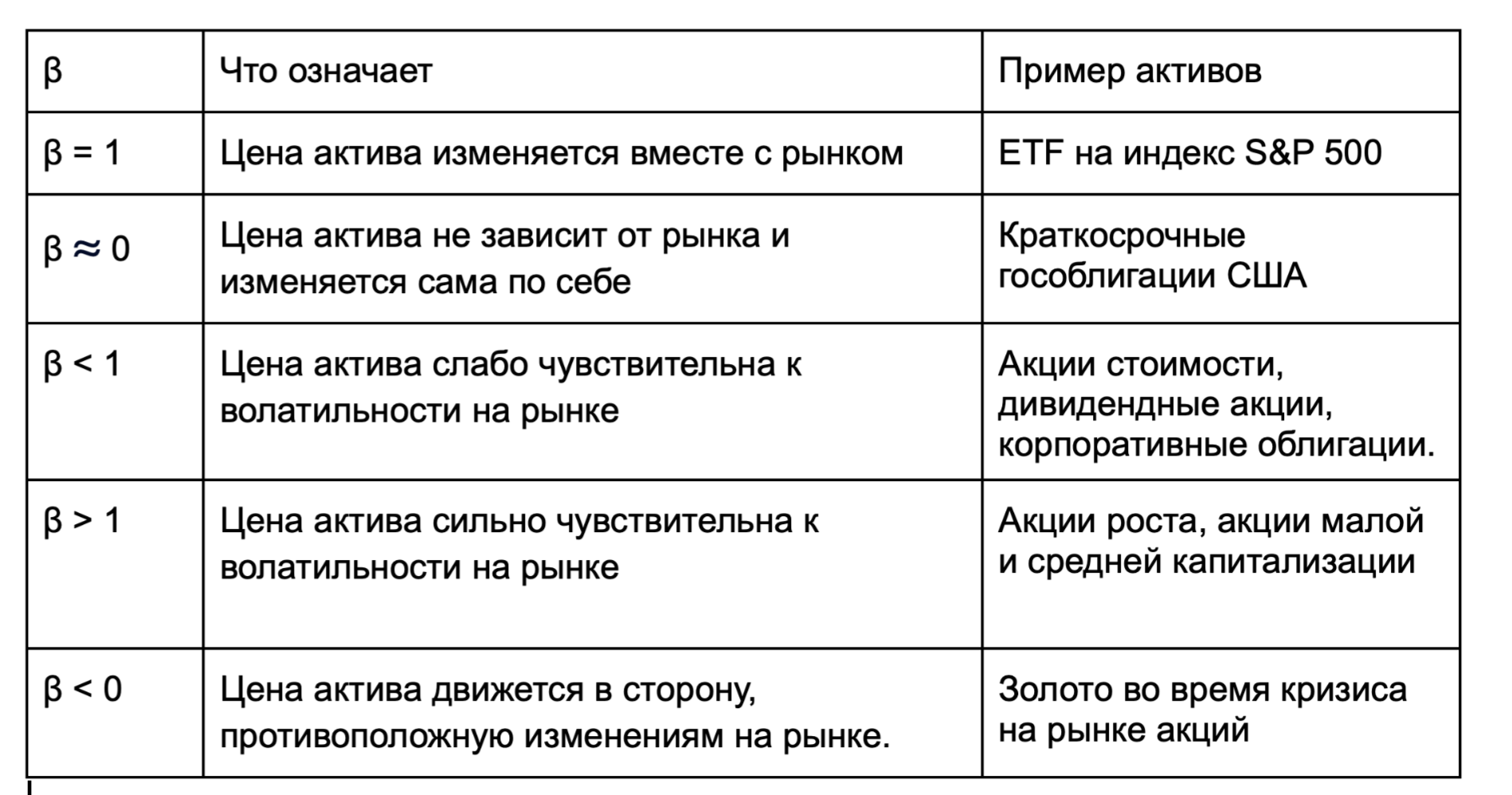
Например, безрисковая ставка принимается равной 3%, ожидаемая доходность рыночного портфеля равна 9%, а бета портфеля —- 1,2. В таком случае ожидаемая доходность портфеля инвестора равна 10,2%. Именно такую доходность должен приносить портфель, чтобы риск был оправдан. Если фактическая доходность окажется меньше, например 8% — инвестор взял на себя повышенные риски, которые не оправдываются полученной доходностью.

В таком случае, инвестор должен пересмотреть структуру своего портфеля на основании данных модели. Это можно сделать, снизив бету портфеля (взяв менее рискованную комбинацию активов) или повысив ожидаемую доходность (добавив в портфель высокодоходные активы, соответствующие уровню риска).

Value at Risk (VaR)

Модель Value at Risk (VaR) показывает размер возможных потерь при данной структуре портфеля с заданной вероятностью за определенный период. Простыми словами, она отвечает на вопрос: какой максимальный убыток портфеля в процентах возможен в 95% случаев за 1 день (неделю, месяц и т.д.). 

Для ответа на этот вопрос VaR статистически рассматривает различные сценарии изменения доходности за исключением редких экстремальных событий на рынке (крах пузыря, паника, начало войны и т.д). Именно поэтому в VaR принимается вероятность равная 95% и 99% (доверительный уровень), в которых исключены редкие случаи. Из оставшихся “нормальных” сценариев модель выбирает худший и оценивает возможные потери.

Формула модели выглядит так: 

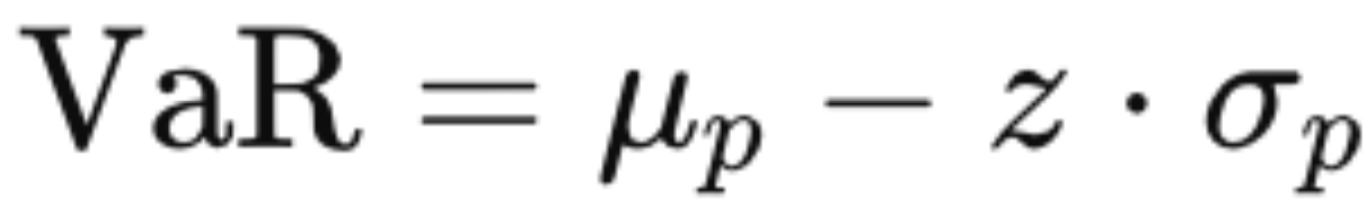
• μp— ожидаемая доходность портфеля за выбранный период,
• σp— стандартное отклонение (волатильность) портфеля за тот же период,
• z — значение квантиля нормального распределения (табличный коэффициент, соответствующий выбранному доверительному уровню, например, 1,65 для 95% и 2,33 для 99%).

В результате расчета инвестор получает максимально возможный убыток в процентах. Например, портфель активов на $10 000 имеет среднедневную доходность за день на уровне 0,05% и волатильность в 1%. С такими данными и доверительным уровнем 95% VaR покажет максимальный возможный убыток в размере 1,6% в день или $1600. Важно учитывать, что реальные убытки с учетом редких случаев (5%) могут быть больше.

Чем меньше максимальный убыток по VaR, тем меньше риски портфеля. Например, дневной убыток в размере 1,6% капитала — это ощутимая просадка. Такой уровень риска обычно выбирают инвесторы с агрессивной стратегией, рассчитывающие заработать на краткосрочных колебаниях цены. 

Активы в консервативных портфелях обычно выбирают с минимально возможными просадками, то есть VaR не должен превышать нескольких десятых долей процента в день или нескольких процентов в месяц.

Симуляция Монте-Карло

Как и VaR, модель симуляции Монте-Карло оценивает возможные сценарии изменения размера капитала в будущем. Главное отличие — вместо статистической оценки одной метрики симуляция Монте-Карло показывает более полную перспективу. 

С ее помощью можно гибко оценить, как стоимость портфеля будет изменяться шаг за шагом при наступлении конкретных событий: высокой волатильности, рыночных шоков, изменений макроэкономических показателей и т.д.

Метод Монте-Карло основан на генерации тысяч возможных сценариев поведения стоимости портфеля при заданных параметрах. Формула расчета стоимости портфеля основывается на геометрическом броуновском движении и имеет сложную форму:

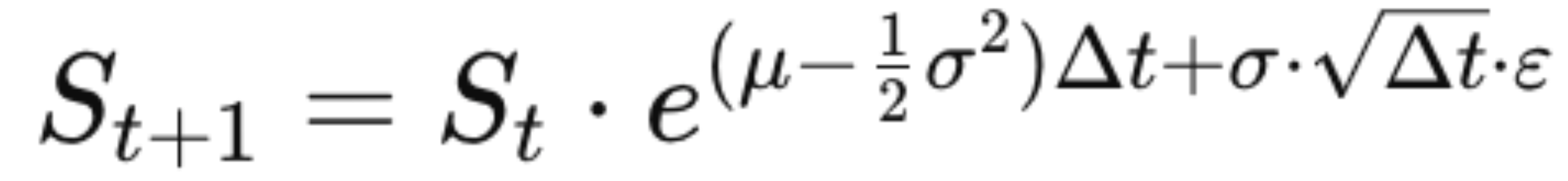
• St— стоимость портфеля в момент времени t
• μ — ожидаемая доходность,
• σ — стандартное отклонение (волатильность),
• Δt — шаг по времени (например, 1/252 для дневных данных),
• ε — случайная величина из нормального распределения.

С помощью заданных параметров и нормального распределения модель генерирует тысячи случайных сценариев движения доходности. Затем она анализирует итоги: например, сколько раз просадка портфеля превысила 10% или сколько раз прибыль была выше 20%.

Например, стартовая стоимость портфеля равна $100 000, рассматриваемый период — 1 год, среднегодовая доходность равна 6%, а волатильность — 10%. При 10 000 симуляций модель даст такие результаты:

• В 5% самых худших случаев убыток превысит $12000
• В 50% случаев изменение окажется в интервале от –$2000 до +$8000
• В 5% лучших случаев прибыль превысит $15000

Такие результаты модели Монте-Карло означают, что просадка в размере $12000 (12%) слишком велика для консервативного портфеля. Этот показатель 5% самых худших случаев в этой модели аналогичен показателю VaR при доверительном интервале 95%. Если цель портфеля — сохранение капитала, именно этот показатель важен для минимизации рисков.

При этом основная масса случаев (50%) говорит об умеренном коридоре доходности от -2% до 8%. Это означает, что портфель может дать устойчивый умеренный рост. Этот показатель важен для портфелей со стратегией сбалансированного роста. Если инвестор готов взять на себя риски этого портфеля, он может рассчитывать на положительную доходность в большинстве случаев.

Третий результат модели Монте-Карло — показатель вероятности получения максимальной прибыли. У портфеля в примере есть потенциал получения прибыли выше 15%, но они сопряжены с рисками убытков.

Ограничения математических моделей оценки рисков

При оценке рисков портфеля нужно учитывать, что математические модели имеют ограничения. Несмотря на то, что формулы рассчитываются на основе реальных данных, они имеют упрощения и допущения. Поскольку реальная ситуация на рынке всегда сложнее любого моделирования, эти оговорки могут снижать точность результатов. 

Например, модель Марковица предполагает, что инвестор всегда рационален и стремится к наилучшему соотношению риска и доходности. На самом деле инвесторы склонны к эмоциям и когнитивным искажениям, которые влияют на принятие решений и восприятие результатов инвестиций.

Помимо игнорирования поведенческих факторов, математические модели оценки рисков портфеля имеют следующие ограничения:

1. Зависимость от исторических данных. Исторические значения цен активов позволяют оценить лишь прошлый уровень рисков и доходности. Ни одна модель не способна предсказать движение цен и наступление кризисных событий, хотя с помощью моделей VaR и Монте-Карло можно оценить их вероятность.
2. Используемые параметры непостоянны. Волатильность, доходность, корреляция между активами и другие параметры постоянно изменяются во времени. Для удобства расчета в математических моделях их считают фиксированными, но это допущение снижает точность оценки.
3. Линейная зависимость параметров. В моделях Марковица и CAPM переменные считаются зависящими друг от друга линейно. На реальном рынке, особенно в кризис, их зависимость может быть нелинейной.
4. Нормальное распределение. Модели VaR, Монте-Карло и CAPM исходят из статистически нормального распределения доходностей (то есть в соответствии с идеально симметричной кривой Гаусса). В реальности кривая распределения не идеальна: у доходностей часто бывают “толстые хвосты” в менее вероятных случаях, то есть экстремальные события могут происходить гораздо чаще.

Несмотря на эти ограничения, математические модели дают хорошие результаты и используются многими профессиональными инвесторами. Они систематизируют подход к управлению рисками, позволяют строить прогнозы, сравнивать портфели и оптимизировать их по заданным параметрам. Для большей точности профессионалы дополняют результаты моделирования экспертными оценками, анализом рыночной ситуации и стресс-сценариями.

Заключение: как инвестору использовать математические модели оценки рисков

Математические модели оценки рисков позволяют оптимизировать структуру портфеля, сравнить активы между собой и принять более рациональные инвестиционные решения. Чтобы избежать ошибок и верно оценивать риски необходимо:

1. Понимать назначение моделей. Каждая модель имеет свои особенности и цели. Модель Марковица применяется для оптимизации структуры, CAPM — для оценки чувствительности к рынку, VaR — для расчета возможных потерь, а Монте-Карло — для анализа множества сценариев.
2. Учитывать ограничения моделей. Реальность на рынке всегда сложнее математических формул. Применяя модели для оценки рисков, нужно учитывать их ограничения и не воспринимать их результат со стопроцентной точностью.
3. Комбинировать модели. Оценивать риски портфелей можно с помощью множества моделей и показателей. Например, модель Марковица можно сочетать с VaR: так можно найти не только вариант портфеля с низкими рисками, но и оценить его возможные убытки.
4. Использовать другие аналитические методы. Чтобы снизить риск ошибок, количественные методы оценки нужно совмещать с качественными. Экспертные оценки и другие аналитические методы делают понимание рынка более многомерным.
5. Регулярно пересматривать параметры. Все переменные из математических моделей постоянно меняются. При изменении рыночной ситуации все показатели нужно расчитывать снова.